Emmanuel College scientists, Martin Nowak and Ben Allen (Researcher) developed an algorithm to predict whether a social structure is likely to favor cooperation. Their findings suggest strong pairwise relationships, rather than loose scattered networks, are more favorable for cooperation.
Professor Allen and his collaborators have derived a condition for when cooperative behaviors will be able to spread across a network via natural selection. Using mathematical modeling, they have found that cooperation flourishes when there are strong pairwise ties between individuals. These “individuals” may refer to people interacting in networks, or other types of organisms in spatially structured habitats.
“We now have a method for determining which networks promote the evolution of cooperation,” said Allen. “If all individuals are equally connected to all others, then selfish behaviors can take over. But if each individual has a just small number of close pairwise ties, cooperation can easily spread from one individual to another. This is an intriguing mathematical argument for the importance of stable partnerships in cooperative societies.”
A “graph” is a mathematician’s term for a network—a set of nodes connected by links. Graphs can be used to represent spatially structured populations. Martin spoke about his 2006 result with Hisashi Ohtsuki that, if all nodes have the same degree (=number of neighbors), the evolution of cooperation is favored (on large graphs, under weak selection, for a particular process), if the benefit-cost ratio is greater than the degree. Yau, who was interested in applying differential geometry tools to the discrete setting of graphs, approached Martin for a potential collaboration.
Yau and Martin assembled a team that included myself, Gabor Lippner (a former postdoc of Yau’s), and Yu-Ting Chen, a probability theorist who was visiting at the CMSA. Each week, we filled a blackboard with equations. With such diverse backgrounds, it took us months to converge on a common language and set of problems.
Eventually, we began to look into the possibility of extending Martin’s 2006 result to the general case in which each node can have a different degree. This problem had been open for a decade, and was thought by many (including myself) to be intractable. Indeed, it was recently discovered that to find an efficient algorithm for the general problem of games on graphs for arbitrary selection strength would imply that P=NP, which the vast majority of mathematicians and computer scientists believe not to be the case.
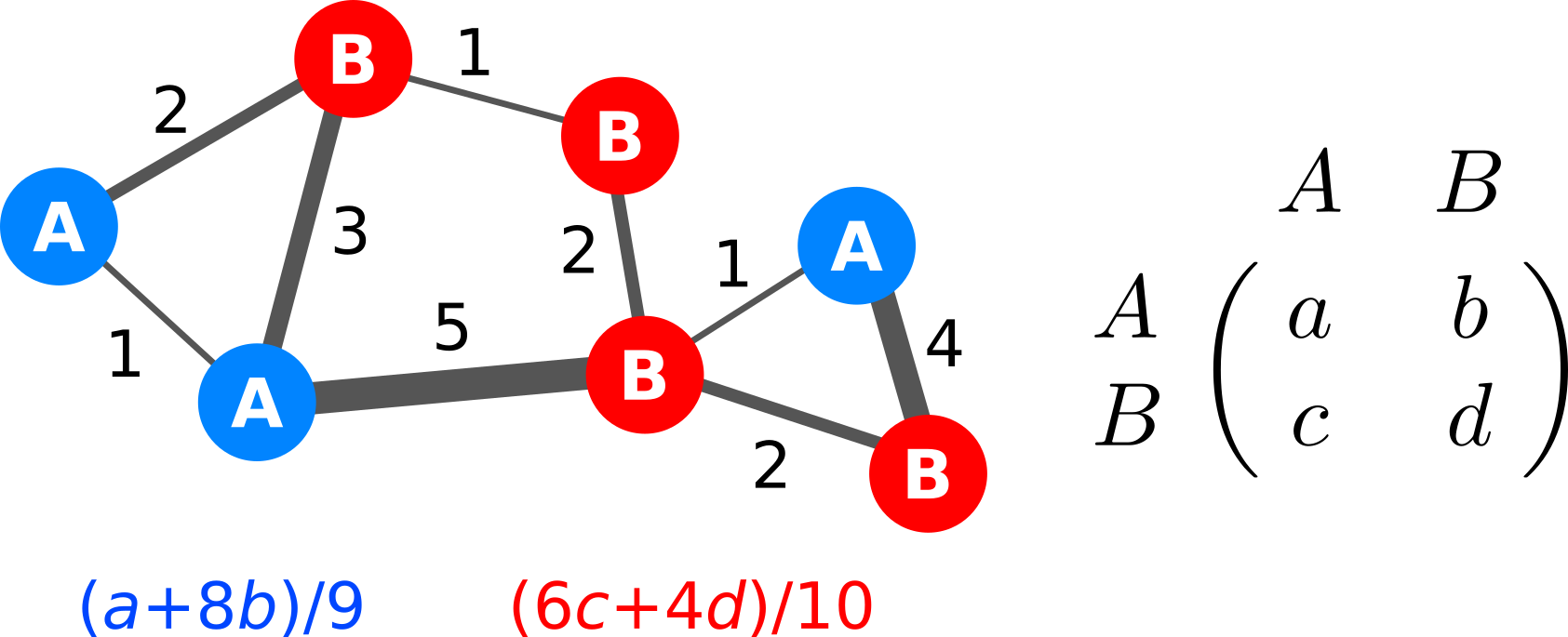
Evolution occurs in populations of reproducing individuals. The structure of a population can affect which traits evolve1, 2. Understanding evolutionary game dynamics in structured populations remains difficult. Mathematical results are known for special structures in which all individuals have the same number of neighbours.
The general case, in which the number of neighbours can vary, has remained open. For arbitrary selection intensity, the problem is in a computational complexity class that suggests there is no efficient algorithm. Whether a simple solution for weak selection exists has remained unanswered. Here we provide a solution for weak selection that applies to any graph or network. Our method relies on calculating the coalescence times of random walks. We evaluate large numbers of diverse population structures for their propensity to favour cooperation. We study how small changes in population structure—graph surgery—affect evolutionary outcomes.
We find that cooperation flourishes most in societies that are based on strong pairwise ties.
Professor Allen’s research was conducted through collaboration with top scholars in the field, including Dr. Shing-Tung Yau, the William Caspar Graustein professor of Mathematics at Harvard and winner of the Fields Medal, the most prestigious prize given in mathematics; and Dr. Martin Nowak, professor of Mathematics and Biology at Harvard University and director of the Program for Evolutionary Dynamics. Also collaborating on this project were Dr. Gabor Lipper, assistant professor of Mathematics at Northeastern University; Dr. Yu Ting-Chen, assistant professor of Mathematics at the University of Tennessee; Dr. Babak Fotouhi, post-doctoral researcher for Harvard University’s Program for Evolutionary Dynamics; and Naghmeh Momeni, a graduate student at McGill University.
“Professor Allen’s latest research on evolutionary dynamics exemplifies Emmanuel’s commitment to interdisciplinary scholarship,” said Emmanuel’s Vice President of Academic Affairs and Dean, William C. Leonard, Ph.D. “Our faculty and students are constantly pushing the boundaries of inquiry through involvement in collaborative research projects across a wide range of industries and disciplines.”
Credit : Emmanuel College
